题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
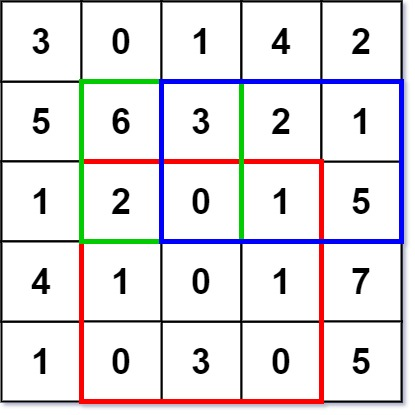
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10⁵ <= matrix[i][j] <= 10⁵
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 10⁴ 次 sumRegion 方法

注意：本题与主站 304 题相同： https://leetcode-cn.com/problems/range-sum-query-2d-immutable/

题解

class NumMatrix {
    /**
     * 存储矩阵的前缀和
     */
    int[][] prefixSum;

    public NumMatrix(int[][] matrix) {
        int rows = matrix.length, columns = matrix[0].length;
        this.prefixSum = new int[rows + 1][columns + 1];
        // 前缀和初始化
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                // 按照矩阵行累加前缀和
                // 第二行前缀和包含第一行的和
                // 减少循环遍历
                this.prefixSum[i + 1][j + 1] =
                    // 减去重复的左上角矩阵和
                    this.prefixSum[i][j + 1] + this.prefixSum[i + 1][j] - this.prefixSum[i][j] + matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return
            // 右下角到起点矩阵和
            this.prefixSum[row2 + 1][col2 + 1]
                // 左上角(第一个行列减1)重复减的部分
                + this.prefixSum[row1][col1]
                // 第一个行减1列 第二个列不变
                - this.prefixSum[row1][col2 + 1]
                // 第二个行不变 第一个列减1
                - this.prefixSum[row2 + 1][col1];
    }
}